System of linear equations with two unknown variables
Using the substitution method or reduction method, find the solutions to the following system, where x and y are integers
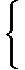
|
5 x - 5 y = 15 x - 12 y = 14 |
Remember !
Substitution method
Substitution method involves analyzing first the system and chosing a convenient equation to express one unknown variable by using the other variables after which, we replace it in the other equation and we obtain an equation with only one unknown variable, we solve the equation and we find the value of the variable, and we come back to the first equation and determine the the other variable.
Elimination method
Elimination method involves multiplying or dividing in a convenient way an equation o both equations with an integer so that by adding up or by making the difference the equations obtained after the multiplication/division, the terms which contain one unknown variables are reduced. The equation is solved, the value obtained for the variable is replaced in one of the eqautions and the value for the other variable is determined.
Observation: If all the terms which contain uknown variables and the free terms are reduced, the system does not have a unique solution. If all the terms that contain unknown variabled are reduced and only the free terms remain, the system does not have solutions.
Exemple !
Exercise solved using the substitution method
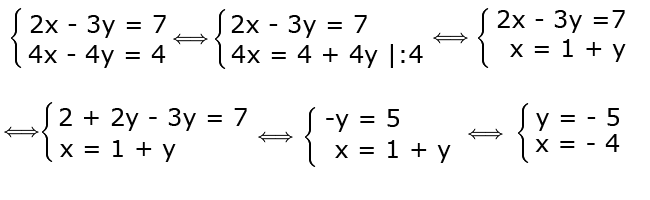
Solution. From the second equation we express x in terms of y, we divide by 4 , we obtain an expression for x, which we use it to substitute x in the first equatio, we determine the value for y, we introduce h value obtained for y in the second equation and we determine x.
Exercise solved using the elimination method
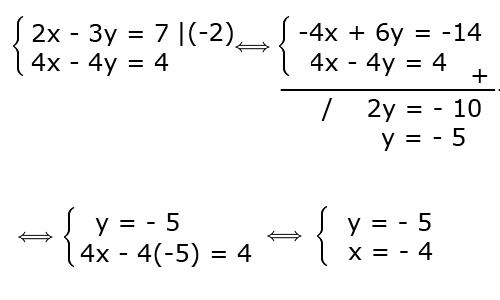
Solution. If we multiply by (-2) the first equation, we can reduce -4x, we add up the equations, we determine y and introduce the obtained value in the second equation and determine x.
Observation. Multiplication with (-2) is not the only method we can use , for example we can multiply the first equation by (-4) and the second by 3 , y is eliminated, but the same result is obtained, the difference between the two methods is only how easy is or not to determine the values for x and y.